Spiegelung 2
Zwar hatte ich Ihnen in der letzten Folge dieser Serie im Heft 1/86 einen Beitrag über Perspektive und ihren hilfreichen Einsatz bei der Lösung von Spiegelungsproblemen angekündigt, doch die in der Zwischenzeit eingegangenen Leser-Reaktionen ließen mich dieses Thema nochmals verschieben.
Vielmehr möchte ich in dieser Folge auf gewölbte Oberflächen eingehen. Wir werden die Frage lösen, was ein Betrachter auf einem bestimmten Punkt einer spiegelnden Fläche sieht, wenn diese nicht eben – wie in der letzten Folge -, sondern eben gewölbt ist.
Wann immer Sie in Zukunft Spiegelungen in gewölbten Flächen darstellen, sollten Sie wenigstens in groben Zügen mit Hilfe der hier gelernten Theorie sicherstellen, dass Sie es auch richtig tun.
Zuerst definieren wir eine gewölbte Oberfläche als Summe vieler Kugelausschnitte mit verschiedenen Radien. Selbst völlig unsymmetrisch geformte Körper lassen sich ja meist auf eine Ansammlung von geometrischen Grundformen zurückführen.
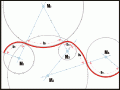 Es vereinfacht die Arbeit erheblich, wenn man ein Gesamtproblem in einzelne Teilprobleme zerlegt. In der Abbildung 1 (rechts) habe ich zum leichteren Verständnis einmal eine komplexe Linie mit Hilfe mehrerer Kreisbögen mit verschiedenen Durchmessern konstruiert. Die für Illustratoren meist unumgängliche zweidimensionale Darstellung einer Kugel ergibt ja in ihren Umrissen bekanntlich einen Kreis.
Es vereinfacht die Arbeit erheblich, wenn man ein Gesamtproblem in einzelne Teilprobleme zerlegt. In der Abbildung 1 (rechts) habe ich zum leichteren Verständnis einmal eine komplexe Linie mit Hilfe mehrerer Kreisbögen mit verschiedenen Durchmessern konstruiert. Die für Illustratoren meist unumgängliche zweidimensionale Darstellung einer Kugel ergibt ja in ihren Umrissen bekanntlich einen Kreis.
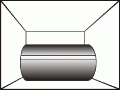 Da ich niemandem, natürlich auch mir selbst nicht, zumuten möchte, alle Gedankenvorgänge ausschließlich im Kopf nachzuvollziehen, habe ich als Arbeitsbeispiel einen recht einfachen Körper (Abb. 2) ausgewählt Daran werden wir in der Praxis jetzt unsere geistigen Höhenflüge verfolgen.
Da ich niemandem, natürlich auch mir selbst nicht, zumuten möchte, alle Gedankenvorgänge ausschließlich im Kopf nachzuvollziehen, habe ich als Arbeitsbeispiel einen recht einfachen Körper (Abb. 2) ausgewählt Daran werden wir in der Praxis jetzt unsere geistigen Höhenflüge verfolgen.
Wir beginnen damit, dass wir an einigen Stellen Schnitte durch den Körper legen. Bedingung für die Richtung der Schnittebene: sowohl der Gegenstand, als auch der Betrachter müssen von ihr geschnitten oder tangiert werden. Man muss dabei nicht übertreiben, was die Menge der Schnittebenen angeht. Einige wenige reichen meist vollständig aus. Die nicht durchkonstruierten Flächenteile können freihändig fertiggestellt werden. Zeichnen Sie dann die Schnittkontur und die Position des Betrachters maßstabsgetreu ein. Auch die Lage der Lichtquelle, beziehungsweise der Lichteinfallswinkel sollten festgelegt werden.
Bitte denken Sie immer daran, dass bei den meisten Illustrationen die Positionen der vier Hauptelemente „Betrachter, darzustellender Gegenstand, Lichtquelle und Umgebung” völlig im Ermessen des Künstlers liegen. Immer wieder habe ich bei meiner Lehrtätigkeit festgestellt, dass Schüler unter sich ihre Aufgabe durch eine komplizierte Komposition unnötig schwer machen. Es ist absolut legitim und „kunstgerecht”, die Komposition dem Motiv anzupassen und nicht umgekehrt.
 Anhand der Schnittebene A aus der Abbildung 3 konstruieren wie jetzt den sichtbaren Bereich der Körperoberfläche und die Spiegelungen aus der Umgebung in ihr. Dazu projizieren wir die Schnittebene in die Zeichnungsebene, sprich: auf unser Blatt Papier (Abb. 4). Verwenden Sie bitte Transparent- oder Layoutpapier, da später noch Arbeitsschritte kommen, bei denen eine Durchsichtigkeit des Papiers zur Vereinfachung erheblich beiträgt.
Anhand der Schnittebene A aus der Abbildung 3 konstruieren wie jetzt den sichtbaren Bereich der Körperoberfläche und die Spiegelungen aus der Umgebung in ihr. Dazu projizieren wir die Schnittebene in die Zeichnungsebene, sprich: auf unser Blatt Papier (Abb. 4). Verwenden Sie bitte Transparent- oder Layoutpapier, da später noch Arbeitsschritte kommen, bei denen eine Durchsichtigkeit des Papiers zur Vereinfachung erheblich beiträgt.
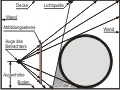 Für den Illustrator reicht es aus, wenn er eine sogenannte „Näherungslösung” für sein Problem bekommt. Es würde im Rahmen dieses Artikels viel zu weit führen, den geometrisch hundertprozentig richtigen Lösungsweg aufzuzeigen und womöglich auch noch zu beweisen. Dies überlassen wir getrost den Mathematikern.
Für den Illustrator reicht es aus, wenn er eine sogenannte „Näherungslösung” für sein Problem bekommt. Es würde im Rahmen dieses Artikels viel zu weit führen, den geometrisch hundertprozentig richtigen Lösungsweg aufzuzeigen und womöglich auch noch zu beweisen. Dies überlassen wir getrost den Mathematikern.
Wichtig für die Konstruktion ist immer die Lage der Mittelpunkte der einzelnen Kreisbögen, aus der sich die Schnittlinie zusammensetzt. Sie zu finden verrate ich Ihnen einen ganz einfachen Trick. Zeichnen Sie auf einem zweiten Bogen mehrere konzentrische Vollkreise mit wachsenden Radien. Legen Sie dann dieses Blatt unter Ihre Schnittlinienzeichnung und verschieben Sie beides solange gegeneinander, bis irgendeiner der Kreise sich mit einem möglichst großen Teil der Schnittlinie deckt Markieren Sie die deckungsgleichen Kreissegmente sowie deren Mittelpunkt.
 Unsere erste Teilaufgabe besteht nun darin, den vom Betrachter aus sichtbaren Bereich der Körperoberfläche einzugrenzen. Dazu konstruiert man die Tangenten, die gleichzeitig auch durch den Standpunkt des Betrachters führen müssen, an die äußeren Kreisbogen. Wie diese Konstruktion gemacht wird, sehen Sie in Abb. 5.
Unsere erste Teilaufgabe besteht nun darin, den vom Betrachter aus sichtbaren Bereich der Körperoberfläche einzugrenzen. Dazu konstruiert man die Tangenten, die gleichzeitig auch durch den Standpunkt des Betrachters führen müssen, an die äußeren Kreisbogen. Wie diese Konstruktion gemacht wird, sehen Sie in Abb. 5.
Verbinden Sie den Mittelpunkt M des in Frage kommenden Kreisabschnittes mit dem Standpunkt P des Betrachters. Diese Strecke wird halbiert und Sie erhalten den Punkt Mr. Zeichnen Sie jetzt einen Kreis um Mr, der durch die beiden Punkte M und P geht Die Schnittpunkte T1 und T2 sind die beiden möglichen Berührungspunkte der Tangenten.
Der nächste Arbeitsschritt ist komplizierter. Mit Hilfe einiger Sehstrahlen werden wir feststellen, welcher Bereich des Hintergrundes sich in welchem Bereich der Körperoberfläche spiegelt.
Erinnern Sie sich bitte an das 2. Reflexionsgesetz. Es lautet: Der Einfallswinkel eines Licht- oder Sehstrahles ist gleich dem Ausfallswinkel. Wem der Beweis dafür fehlt, oder wer das Gesetz nochmals durcharbeiten möchte, lese bitte in der ersten Folge dieser Serie in Heft 1/86 nach. Die Konstruktion der Ein- und Ausfallswinkel an einer ebenen Fläche wurde dort auch gezeigt.
 Wie konstruiert man zwei gleiche Winkel an einer gewölbten Oberfläche? In Abbildung 6 können Sie die Konstruktion für einen einzelnen Strahl nachvollziehen. Zeichnen Sie bitte zuerst einmal den einfallenden Sehstrahl auf einen bestimmten Punkt der gebogenen Fläche. Im Beispiel ist das die Linie PB.
Wie konstruiert man zwei gleiche Winkel an einer gewölbten Oberfläche? In Abbildung 6 können Sie die Konstruktion für einen einzelnen Strahl nachvollziehen. Zeichnen Sie bitte zuerst einmal den einfallenden Sehstrahl auf einen bestimmten Punkt der gebogenen Fläche. Im Beispiel ist das die Linie PB.
Danach verbinden Sie den Mittelpunkt M des Kreises mit dem Auftreffpunkt B des Sehstrahles und verlängern diese Linie h über B hinaus. Der Winkel a1 ist der Einfallswinkel. In dieser Zeichnung wird übrigens sehr schön klar, warum der Einfallswinkel immer an der Senkrechten im Einfallspunkt gemessen wird.
Zum Antragen des Ausfallwinkels a2 reichen nun zwei Zirkelschläge. Stechen Sie mit einem beliebigen Radius im Punkt B ein und zeichnen einen Halbkreis. Dieser schneidet die Linie h im Punkt Mh und den einfallenden Sehstrahl im Punkt S1. Ziehen Sie einen Kreis um den Punkt MH mit dem Radius m und es ergibt sich als Schnittpunkt der beiden letzten Kreise der Punkt S2. Verbinden Sie nur noch B mit S2 und Sie haben die Richtung des ausfallenden Sehstrahles.
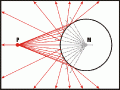 Nachdem die Konstruktion für einen Strahl klar ist, sollte auch die für ein Bündel von Strahlen keine Schwierigkeiten mehr bereiten. In der Abbildung 7 sehen Sie ein Beispiel.
Nachdem die Konstruktion für einen Strahl klar ist, sollte auch die für ein Bündel von Strahlen keine Schwierigkeiten mehr bereiten. In der Abbildung 7 sehen Sie ein Beispiel.
Jetzt haben wir also eine doch recht kompliziert aussehende Zeichnung – was können wir damit anfangen?
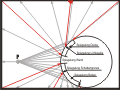 Zum Weiterarbeiten müssen wir die Gesamtkomposition der Illustration mit einbeziehen. Stellen Sie also die gerade angefertigte Zeichnung einmal in die Umgebung, die Sie sich für Ihre Illustration ausgedacht haben, wie in Abbildung 8.
Zum Weiterarbeiten müssen wir die Gesamtkomposition der Illustration mit einbeziehen. Stellen Sie also die gerade angefertigte Zeichnung einmal in die Umgebung, die Sie sich für Ihre Illustration ausgedacht haben, wie in Abbildung 8.
Selbst wenn die von Ihnen konstruierten Sehstrahlen nicht genau auf ein Objekt aus der Umgebung Ihres Motivs gerichtet sind, können Sie dennoch dessen Spiegelung in der Oberfläche schon recht genau bestimmen. Sie müssen lediglich die fehlenden Verbindungen zwischen einzelnen, dank der genauen Konstruktion festliegenden Punkten, einzeichnen. Der Mathematiker nennt diese Technik interpolieren.
Da die konstruktive oder rechnerische Interpolation viel zu aufwendig wäre, verlassen wir uns bei diesen Zwischenschritten auf unsere Erfahrung. Die Verbindungen zwischen den einzelnen sicher ermittelten Punkten wird also „frei Hand” eingezeichnet.
Für unser Beispiel habe ich mir einen fiktiven Raum ausgedacht mit Boden, Wand und Decke. Wie Sie sehen, werden die Ecken natürlich nicht von einem der vorher konstruierten Sehstrahlen genau getroffen. Trotzdem können wir den Abbildungspunkt auf der spiegelnden Oberfläche – zumindest näherungsweise – relativ leicht einzeichnen. Wer’s ganz genau wissen will, müsste jetzt noch mehr Strahlen in Richtung auf die Raumkanten einkonstruieren.
Auch die Spiegelung der Lichtquelle in der Körperoberfläche kann auf diese Art und Weise bestimmt werden. Markieren Sie sich die wichtigsten Bereiche und Punkte der Spiegelung in Ihrer Schnittzeichnung.
Da die genaue Lage von Motiv und Lichtquelle ja gegeben war, ist es ein Leichtes, auch den Schatten zu konstruieren. In Abbildung 8 habe ich ihn eingezeichnet. Natürlich spiegelt sich dieser Schatten auch auf dem Spiegelkörper.
Je glatter übrigens eine Fläche ist, desto scharfkantiger bildet sich die Umgebung in ihr ab. Der Illustrator ist in der glücklichen Lage, solche Überschärfen noch extremer darzustellen, als zum Beispiel der Fotograf. Nutzen Sie diesen Umstand weidlich aus. Allerdings sollte man auch nicht übertreiben. Das richtige Mittelmaß zu finden, ist Erfahrungssache – dafür habe ich keine Regel.
Die letzte nötige Konstruktion besteht in der Rückführung der Schnittzeichnung in die ursprünglich dreidimensionale Abbildung. Nehmen Sie diese Transformation nach Augenmaß vor.
Nachdem nun die Spiegelungen im Motiv eingezeichnet und mit Hilfe von ein klein wenig Theorie untermauert worden sind, müssen Sie nur noch die Farbe ins Spiel bringen.
Sehr wichtig bei spiegelnden Oberflächen: die gesamte Umgebung spiegelt sich in ihren Originalfarben, wenn das Material des Körpers keine Eigenfarbe besitzt. In unserem Beispiel bin ich von Chrom ausgegangen, darum gebe ich auch die Originalfarben wieder. Bei farbigen Spiegeln müssen Sie die Originalfarbe so darstellen, als würden Sie sie durch einen Filter von der Eigenfarbe des Spiegelmaterials betrachten. Beispiel Gold: blauer Himmel wird leicht grünstichig.
Die letzte Anweisung gehört eigentlich schon gar nicht mehr in die Spiegelungstheorie, sondern zum Thema Farbe. In einem der nächsten Hefte der Airbrush-Zeitung werde ich im Zusammenhang mit der Serie „Farbe” einmal darauf eingehen.
Für diesmal habe ich ihnen hoffentlich genug „Futter” gegeben. Bleibt mir nur noch, Ihnen viel Vergnügen zu wünschen – und sollten Sie einmal einen Einfallswinkel vor lauter Ausfallswinkeln nicht mehr finden, bleibt Ihnen immer noch die „empirische” Methode: Probieren geht über Studieren!

